Изобретатель Владимир Ковальджи предлагает полезное и увлекательное применение набора магнитов «Многопользовательский Тетриус» — головоломки-симметриксы и соревнования по поиску их решений в школе или офисе.
Симметриксы — головоломки, в которых нужно сложить симметричную фигуру. Симметриксы придумал японский изобретатель Тадао Китазава в 2003 году, и многие исследователи подхватили его идею, в том числе русские изобретатели Геннадий Яровой и Владимир Красноухов. В настоящее время ни один чемпионат по пазлспорту не обходится без симметриксов.
Элементы симметриксов бывают самой разной формы. Некоторые головоломки, и «Тетриус» тоже, включают несколько полимино — фигурок, которые состоят из соединенных сторонами квадратов (как шахматные клетки, по которым ходит ладья).
«Многопользовательский Тетриус» состоит из трех комплектов по семь тетрамино — фигурок из четырех квадратов. В головоломках-симметриксах элементы поворачиваются как угодно, поэтому значимых фигур получается пять.

Фигура, составленная из тетрамино, тоже должна представлять собой полимино, то есть клетки элементов должны граничить только целой стороной.


Элементы разрешается вертеть и переворачивать, но нельзя накладывать друг на друга. Если в фигуре есть «дырки», они тоже должны быть включены в общую симметрию.
На сегодняшний день Владимиру Ковальджи удалось составить 89 симметричных фигур. Это уже очень много, а сколько еще не найдено — сказать трудно. Тем, кто серьезно увлекся симметриксами на основе тетрамино, рекомендуется завести альбом и фиксировать в нем свои решения.
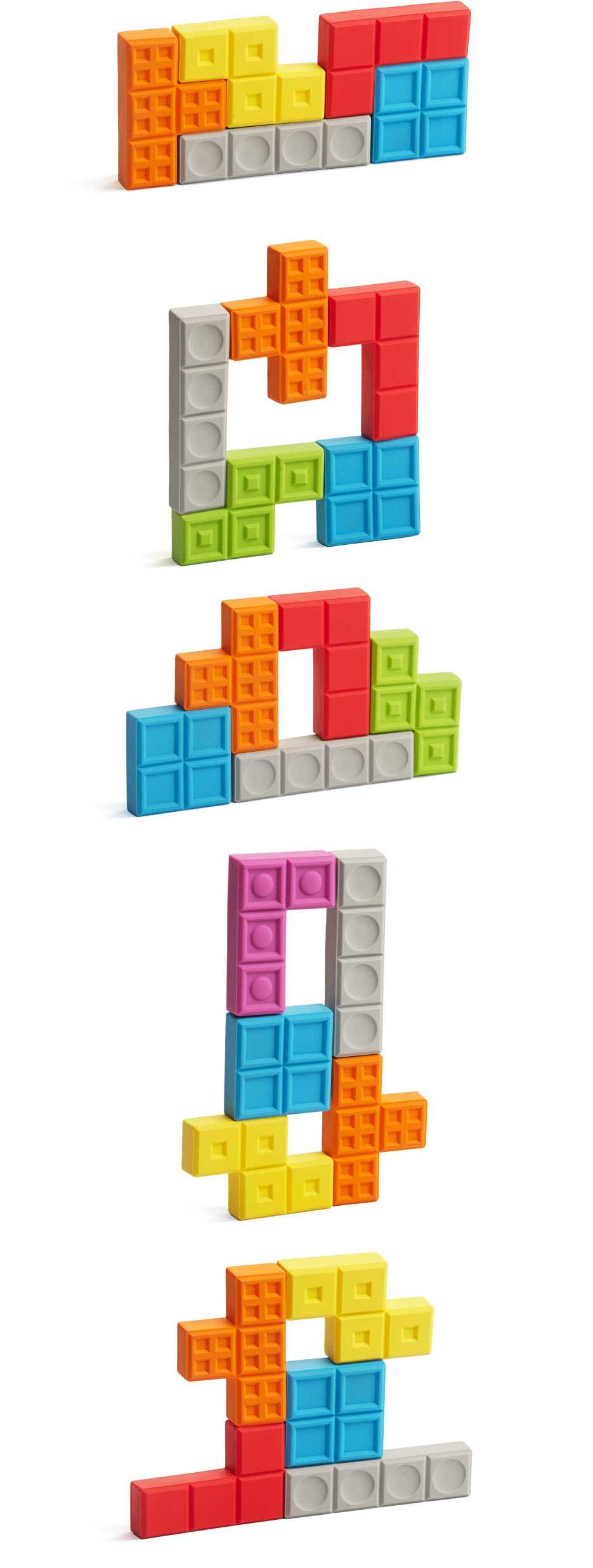
Интересной и часто сложной задачей является поиск симметриксов из различных комбинаций трех или четырех фигурок-тетрамино.

Задания
Перед складыванием симметричных фигур из элементов «Тетриуса» полезно вспомнить, какой бывает симметрия: осевая — две половинки фигуры отражаются друг в друге относительно прямой; центральная — любая точка фигуры имеет напарницу, симметричную относительно определенной точки (центра); вращательная и другие.
В одних случаях ось симметрии проходит параллельно сторонам клеток (как в левой фигуре на первом рисунке). Такая симметрия называется прямой. В других случаях ось симметрии проходит по диагоналям клеток (как в правой фигуре на первом рисунке) — такая симметрия называется диагональной. Ось симметрии всегда одна. Центральная симметрия встречается редко, но тем интереснее ее находить.
Задача поиска симметричных фигур поначалу кажется простой, но в ней есть подводные камни. Дело в том, что симметрию надо научиться видеть. Многие люди в процессе составления получают симметричную фигуру, но попросту не замечают ее, поэтому полезно сперва потренироваться на минимальных наборах.
Все задания, начиная с 9-го, отлично подходят для групповых соревнований по поиску большего числа решений за определенное время (например, за час).
1. Для разминки стоит попробовать найти все возможные симметричные фигуры, состоящие всего из двух элементов (две из них показаны выше). Например, из фигурок L и S составляются две фигуры.

2. Найти три симметричные фигуры из трех элементов — I, T и S (прямая симметрия).
3. Найти две симметричные фигуры из трех элементов — I, L, S (диагональная симметрия).
4. Найти три симметричные фигуры из трех элементов — L, S, O.
5. Найти пять симметричных фигур из трех элементов — L, S, T.
6. Найти шесть симметричных фигур из трех элементов — I, L, T.
7. Найти две симметричные фигуры из трех элементов — I, S, O. Первое решение (прямая симметрия) находится легко, а второе очень трудно.
Все наборы из двух или трех тетрамино позволяют собирать фигуры исключительно с осевой симметрией (прямой или диагональной), и только здесь единственный раз встречается центральная.
8. Найти четыре симметричные фигуры из четырех элементов — I, S, T, O.
Для этой и последующих задач точное число решений не определено. Возможно, читателям удастся найти больше симметричных фигур из указанных элементов.
9. Найти девять симметричных фигур из четырех элементов — I, L, T, O.
10. Найти одиннадцать симметричных фигур из четырех элементов — L, S, T, O.
Этот набор сложен, но он является ключом примерно к четверти решений задач со всеми пятью тетрамино — не хватает только фигуры I, прибавление которой к этим 11 решениям с разных сторон автоматически дает 23 решения для пяти элементов. Чтобы понять, почему 23, а не 22 (11 × 2), нужно найти все решения.
11. Найти восемь симметричных фигур из четырех элементов — I, L, S, O.
12. Найти все симметричные фигуры из четырех элементов — I, L, S, T.
Удивительно, но именно самая симметричная фигура О (квадрат — целых четыре оси симметрии) является самой «мешающей» — без нее решений получается гораздо больше (от 34 и выше).
13. Найти две симметричные фигуры с максимально большой «дыркой» из четырех элементов — I, L, S, T.
В данном случае это «дырка» площадью в 4 клетки.
14. Найти две симметричные фигуры с двумя «дырками» из четырех элементов — I, L, S, T.
15. Найти самую длинную симметричную фигуру из четырех элементов — I, L, S, T.
Возможны решения длиной от 9 клеток.
16. Найти пять симметричных фигур с максимально большой «дыркой» из всех пяти элементов — I, L, S, T, О.
В данном случае это дырка площадью в 6 клеток.
17. Найти 11 симметричных фигур с двумя «дырками» из всех пяти элементов — I, L, S, T, О.
18. Найти три симметричные фигуры с двумя «дырками» разного размера из всех пяти элементов — I, L, S, T, О.
19. Найти симметричную фигуру с самой длинной «дыркой» из всех пяти элементов — I, L, S, T, О.
Длина в 3 клетки получается легко, возможна ли большая?
Головоломки с использованием всех семи тетрамино имеют огромное количество решений и являются скорее игрой, если не ставить задачей поиск фигур с фиксированными свойствами («дырками» определенного размера и прочим).
Также со всеми семью фигурами легко создавать задания для детей, сходные со знаменитым «Танграмом». Нужно заранее составить и зарисовать контуры разных красивых фигур (необязательно симметричных, допускается просто особая форма — котик, домик и т. п.), а участники должны постараться сложить их из «Тетриуса». Или каждый участник сам придумывает фигуру и обводит ее контур, а другой потом старается воссоздать ее с помощью «Тетриуса».